Squircle 이란?
플러터로 sliver 리스트를 구현하던 중 corner radius 값을 주어 끝을 둥글게 만드는 코드를 작성했다. 하지만 막상 실기기로 돌려보니 끄트머리가 묘하게 각져있는 것을 확인할 수 있었다. 앱 디자인이 전반적으로 "둥글둥글" 느낌이 나야하는데 먼가 SwiftUI에서 구현했을 때랑 느낌이 달랐다.. 분명 SwiftUI는 CornerRadius값만 주어도 둥글둥글한 느낌이 살아있었다. 백문이불여일견, 바로 같은 Corner Radius를 주어 SwiftUI와 Flutter를 비교해보았다.


역시 애플 갓
위는 SwiftUI 코드로 작성한 Rounded Container이고 아래는플러터로 작성한 Rounded Container이다. 자세히 들여다보면 플러터 모서리가 묘하게 각져있음을 확인할 수 있다. (스크린샷을 찍어서 차이가 안날수도 있지만ㅠ 실기기를 돌려보면 분명한 차이가 난다.) 왜 똑같이 corner radius 값을 주었음에도 SwiftUI에서 더 귀여운 컨테이너가 만들어지는걸까?

애플 내부 코드로 들어가보았지만 감춰져있어서 직접적인 확인은 할 수 없었다. 하지만 RoundedCornerStyle을 enum으로 circular와 continuous로 나누어서 구현할 수 있었는데 flutter의 모서리에 Squircle을 적용하면 SwiftUI의 continuous와 같은 효과를 줄 수 있다는 것을 알게되었다. Squircle 이란 무엇인지 알아보자

Squircle은 사각형과 원 사이의 도형으로 정점을 서로 연결할 때 완전히 둥글게도, 직선도 아닌 "완만하게"연결한 도형이다. 이때 모서리 구현에 있어서 보통 타원처럼 깎이게 되는데 Squircle은 타원보다 더 완만하게 곡선을 그리게 된다.
혹시 여기까지 읽으면서 아니 이게 먼차이인지 전혀모르겠는데? 싶으면 아이폰이나 맥을 이용했을 때의 느낌을 생각해보면 좋다. 애플제품을 이용할때 다른제품과 다르게 묘하게 곡선감이 살아있는 부분을 느낄 수 있다. (앱이라든지, 에어팟 프로 케이스같은 하드웨어든지) 실제로 피그마 공식블로그에 따르면 iOS디자인시스템에 squircle이 핵심적으로 도입된다고 한다. RoundedCornerStyle.continuous도 이러한 애플의 디자인 철학이 들어간 예시라고 볼 수 있다.
그래서 그런지 아쉽게도 구글이 만든 플러터에서는 이러한 곡률감을 프레임워크 차원에서 제공해주지않는다. 하지만 개발자는 도구를 탓하지 않는법, 직접 곡선을 그림으로써 플러터에서도 iOS와 같은 곡률감을 살릴 수 있다. 플러터에서 Squircle 구현을 위해서는 quaraticBezierTo 메서드가 사용되고 이 메서드를 이용하기 위해서는 몇가지 수학개념을 이해해야한다.
타원(elpise)방정식

- 흰 도화지에 두 개의 점(정점)을 찍고 두 개의 점을 실로 연결했다고 생각해보자
- 이 실에 막대기를 최대한땡겨서 원을 그리게 되면 타원이 생겨난다.
- 따라서 타원이란 2개의 정점으로부터 거리의 합이 일정한 점의 집합이다.

2개의 정점 거리의 합이 타원이라는 것을 수식으로 표현하면 위와같이 도출할 수 있다.

코드로 위와같은 타원방정식을 이용해 A점에서 B점으로 연결하는 곡선을 그릴 수 있다.
타원방정식 일반화를 통해 Squircle 방정식 구하기
선형대수학의 P-norm을 이용하면 타원방정식을 일반화할 수 있다. norm이란 (벡터)크기를 나타내는 녀석이다. 벡터는 보통 물리적인 길이를 통해 크기를 비교할 수 있다. 즉 norm은 벡터의 거리를 측정하는 수학적 도구라고 할 수 있다.

일반적인 벡터 길이를 구하는 공식은 2-norm이다. (0,0) 에서 (1, 3) 벡터의 길이는 피타고라스 방정식을 이용해서 루트10임을 할 수 있다. 그렇다면 벡터와 벡터의 거리를 구하는 것을 일반적인 점과 점사이 거리 공식을 사용해서 벡터 사이 거리를 구하게 된다. 이게 2-norm이다. 즉 벡터거리 측정에 있어 2-norm은 유클리드 거리(일반적인 최단거리)와 같다고 볼 수 있다.


1norm은 2norm공식에서 2대신 1을 넣는 방정식으로 표현된다. 이를 시각적으로 표현하면 위 사진에서 맨허튼 거리에 해당한다.


자그러면 이제 일반화를 위해 무한-norm을 보내면 어떻게 될까? 인피니티 놈은 2-norm의 2, 1-norm의 1대신 무한대를 붙여본다고 생각해보자. 극한 성질에 의해 절대값이 가장 큰 놈이외에 나머지 값(x2, x3..)들은 모두 무시된다. 따라서 인피니티 norm은 벡터의 성분중 가장 큰 값을 측정하는 방식이다.

자 그러면 벡터 거리를 고정하고 p-norm이라고 할 때 p의 값에 따라 어떻게 달라지는지 그래프로 확인해보자. 먼저 2-노름을 그려보면 위 방정식에 양항에 제곱을 하고나면 원의 방정식과 같은 것을 확인할 수 있다. 즉 2-norm을 그래프로 표현하면 원이다.

1norm은 어떻게 될까? 위 공식을 보면 알 수 있듯이 그냥 두점을 잇는 공식과 같다는 것을 확인할 수 있다.

마지막으로 인피니티-norm은 어떻게 될까? 벡터크기를 1이라고 했을 때 (1, 0), (1, 1/2), (1, 1/3) 등등 예시를 보면 일단 절댓값이 가장 큰 1로 고정되는 것을 알 수 있다. 즉 벡터크기가 1이면 어차피 x,y좌표 1을 넘지 못하기 때문에 0,0기준 동서남북으로 1만큼 거리가 있는 직사각형이 만들어짐을 확인할 수 있다. 이를 p에따른 그래프를 그려보면 위와같이 확인할 수 있다.

이같은 norm개념을 통해 타원방식을 일반화 해서 적용하면 타원보다 더 완만한 그래프를 그리기 위해 p=2 대신 squircle에서는 p=4를 적용했음을 확인할 수 있다.

Squircle은 수학적인 개념으로 봤을 때 두 벡터 사이 거리(크기) 곡선을 타원보다 더 완만하게 그리는 것이라고 볼 수 있다. 그렇다면 Squircle과 우리가 사용하는 quadraticBezierTo는 무슨 관계일까?
Bezier Curve

quadraticBezier는 Bezier Curve의 한 종류이기 때문에 먼저 베지에커브부터 이해해야한다. 베지에커브는 프랑스 엔지니어 베지에가 고안한 방정식을 따라 그리는 곡선이다. 당연히 "선"이기 때문에 베지에 곡선을 정의하는데는 2개이상의 점이 필요하고 이점을 control point라고 부른다. 2개의 점(point)으로 베지에 곡선을 그리는 기본적인 방정식은 위와같다.

베지에커브는 제어점의 갯수에 따라 종류가 나뉘어진다. 제어점의 갯수가 3개면 quadraticBezier Curve, 제어점이 4개이면 cubic Bezier curve이다.


quadraticBezier Curve 의 방정식은 위와같이 point가 하나 더 늘어난 이차방정식이다.



기존 squircle 방정식(위)에서 x, y로 매개변수화 하면 중간과 같은 식이 도출된다. 여기서 세타(각도)는 90도 각이기 때문에 0부터 π/2 사이 값을 가지게 된다. 이를 한번더 근사값으로 하면 맨아래와 같은식으로 일반화할 수 있다. (테일러 급수 사용)
💡 테일러 급수란?
https://youtu.be/xE0QTkGmIHo?si=yAh4RAoIEeyjR5oL

베지에 커브의 3개의 포인트를 예시와 같이잡고 계산해보자
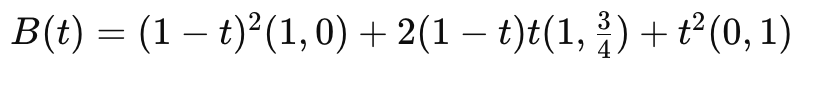


이와 같이 p1의 포인트점을 통해 quadratic 베지에 커브 방정식을 단순화 시킬 수 있다.


이렇게 단순화를 거쳐 베지에 커브를 통해 squircle의 근사값을 얻어낼 수 있게 된다. 그렇다면 왜 quadraticBezier Curve를 사용하냐 더 조절점이 많은 cubic Bezier curve를 사용하는 것이 좋지 않느냐라고 반문할 수 있는데 맞는말이긴하다. 조절점이 많을 수록 Squircle방정식과 더 가까운 근사값을 얻을 수 있기는하다. 하지만 조절점이 늘어날 수록 작성해야할 코드가 너무 복잡해지고 3개의 조절점만으로도 충분히 Squircle 곡선과 유사하게 구현할 수 있다.

드디어 코드를 쳐볼 때가 되었다. 플러터에서 quadraticBezierTo 메서드를 통해 스쿼클을 표현하면 위와 같다. 사용된 메서드를 알아보자면
void quadraticBezierTo(double x1, double y1, double x2, double y2)
final path = Path()
..moveTo(50, 50) // 시작점 (P0)
..quadraticBezierTo(100, 100, 150, 50); // 제어점 (P1), 끝점 (P2)
// 시작점(50, 50), 제어점 (100, 100), 끝점 (150, 50)을 사용한 2차 베지어 곡선quadraticBezierTo 메서드에는 파라미터가 4개가 들어가는데 이는 제어점, 끝점의 x좌표와 y좌표가 들어가기 때문이다. 시작점은 moveTo메서드를 통해 미리 정의해준다. 이때 사이사이 껴잇는 lineTo메서드는 실제로 라인을 그려주는 메서드이다. 즉 위코드에서 각 moveTo 가 시작점을 정해주고 lineTo가 사각형의 직선을 그려주고 직선이 끝나는 지점을 시작점으로 quadraticBezierTo 메서드가 곡선 모서리를 그려준다.
이때 모서리를 둥글게 만드는 반경(borderRadius)이 컨테이너의 너비나 높이보다 크면, 곡선이 컨테이너 밖으로 나가게 되어 깨짐 현상이 발생하기 때문에 조절점의 위치를 clamp 메서드를 통해 컨테이너의 너비나 높이를 넘지 않도록 제한한다.

위 코드를 활용해 Squircle 근사값을 그려낸 컨테이너와 그냥 corner radius값만 준 컨테이너이다. 왼쪽 컨테이너의 모서리가 훨씬 더 통통하고 귀엽게 곡선감이 들어가있고 오른쪽 컨테이너는 약간 각져있고 홀쭉한 곡선이다. 이와 같이 플러터에서도 iOS처럼 Squircle 디자인이 적용된 귀여운 컨테이너를 그릴 수 있다.

여담으로 구글에 검색해보면 스택오버플로우에서는 ClipPath를 통해 스쿼클을 구현한다는 답변이 있었지만 일정 cornerRadius 값이 넘어가면 깨짐 현상이 발생했고 곡선도 iOS처럼 예쁜 곡선이 아닌 각져있는 곡선이 나왔었다.
'Flutter' 카테고리의 다른 글
| Freezed 패키지 사용이유 알아보기 (0) | 2024.08.03 |
|---|---|
| Don't use 'BuildContext's across async gaps 이슈 (0) | 2024.08.01 |
| Shared Preference 패키지를 쓰지말아야하는 이유 (0) | 2024.07.25 |
| flutter 네비게이션바와 버튼의 물결효과 없애기 (feat. inkwell widget) (0) | 2024.07.24 |
| Target of URI doesn't exist: 'firebase_options.dart' 에러 (1) | 2024.07.24 |
